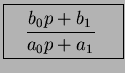 Y(t)
Y(t)
Параметры всех моделей выбраны с учетом реальных характеристик SEW-приводов.
Основой для моделирования приводов является расчет простого апериодического звена:
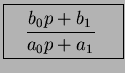 Y(t)
Y(t)
где а и b - параметры апериодического звена.
То есть численное решение дифференциального уравнения 1-го порядка:
| (49) |
Вычисления выполняются по рекурсивной формуле:
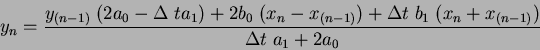 |
(50) |
где:
В настоящее время основой всех моделей приводов является следующий простой элемент:
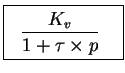
где:
Для моделей приводов A и Z используется еще два алгоритма (элемента)
имитации особенностей реальных приводов. Первый алгоритм это имитация
зоны нечуствительности (т.е. того, что привод начинает отработку со
скорости ![]() ) и ограничение по возможной максимальной скорости
) и ограничение по возможной максимальной скорости
![]() .
.
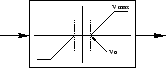
Второй алгоритм это ограничение максимального ускорения и торможения.
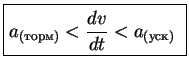
Которые могут объясняться, например, ограничением по максимальному току в реальном приводе.
Для моделей приводов A и Z имитируется останов при переходе из режима наведения в режим ведения, т.е. программа ждет пока модельная скорость отработки упадет до нуля.
Во всех случаях после получения модельной скорости отработки рассчитывается
следующее значение соответствующей модельной координаты. Например:
| (51) |