Previous Section
Part 1: Observations of Global Properties
Part 2: Homogeneity and Isotropy; Many Distances; Scale Factor
Part 3: Spatial Curvature; Flatness-Oldness; Horizon
Part 4: Inflation; Anisotropy and Inhomogeneity
FAQ |
Tutorial :
Part 1 |
Part 2 |
Part 3 |
Part 4 |
Age |
Distances |
Bibliography |
Relativity
Inflation
The "inflationary scenario", developed by Starobinsky and by Guth,
offers a solution to the flatness-oldness problem and the
horizon problem. The
inflationary scenario invokes a
vacuum
energy density. We normally think of the vacuum as empty and
massless, and we can determine that the density of the vacuum is
less than 1E-30 gm/cc now. But in quantum field theory, the vacuum
is not empty, but rather filled with virtual particles:
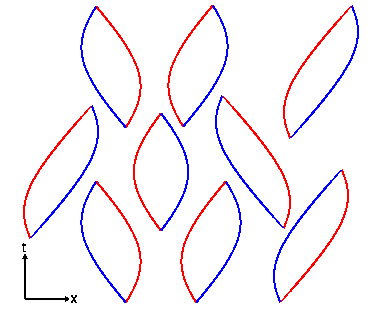
The space-time diagram above shows virtual particle-antiparticle
pairs forming out of nothing and then annihilating back into
nothing. For particles of mass m, one expects about one
virtual particle in each cubical volume with sides given by
the Compton wavelength of the particle, h/mc, where h is
Planck's constant. Thus the expected density of the vacuum
is rho = m4*c3/h3
which is rather large. For the largest
elementary particle mass usually considered, the Planck mass M defined
by 2*pi*G*M2 = h*c, this density is 2E91 gm/cc. Thus the vacuum
energy density is at least 121 orders of magnitude smaller than
the naive quantum estimate, so there must be a very effective
suppression mechanism at work. If a small residual vacuum
energy density exists now, it leads to a
"cosmological constant"
which is one proposed mechanism to relieve the tight squeeze
between the Omegao=1 model
age of the Universe, to = (2/3)/Ho =
10 Gyr, and the apparent age of the oldest globular clusters,
16+/-4 Gyr. The vacuum energy density can do this because
it produces a "repulsive gravity" that causes the expansion of
the Universe to accelerate instead of decelerate, and this
increases to for a given Ho.
The inflationary scenario proposes that the vacuum energy was
very large during a brief period early in the history of the
Universe. When the Universe is dominated by a vacuum energy
density the scale factor grows exponentially,
a(t) = exp(H(to-t)). The Hubble constant really is constant
during this epoch so it doesn't need the "naught".
If the inflationary epoch lasts long enough the exponential
function gets very large. This makes a(t) very large,
and thus makes the radius of curvature of the Universe
very large. The diagram below shows our
horizon superimposed
on a very large radius sphere on top, or a smaller sphere on
the bottom. Since we can only see as far as our horizon,
for the inflationary case on top the large radius sphere
looks almost flat to us.
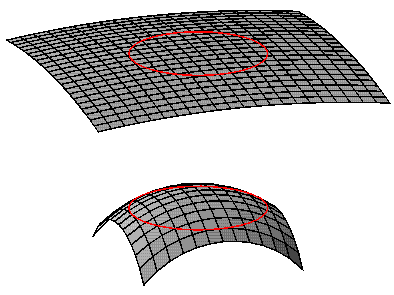
This solves the flatness-oldness problem as long as the exponential
growth during the inflationary epoch continues for at least 100
doublings.
Inflation also solves the horizon problem, because the future lightcone
of an event that happens before inflation is expanded to a huge
region by the growth during inflation.
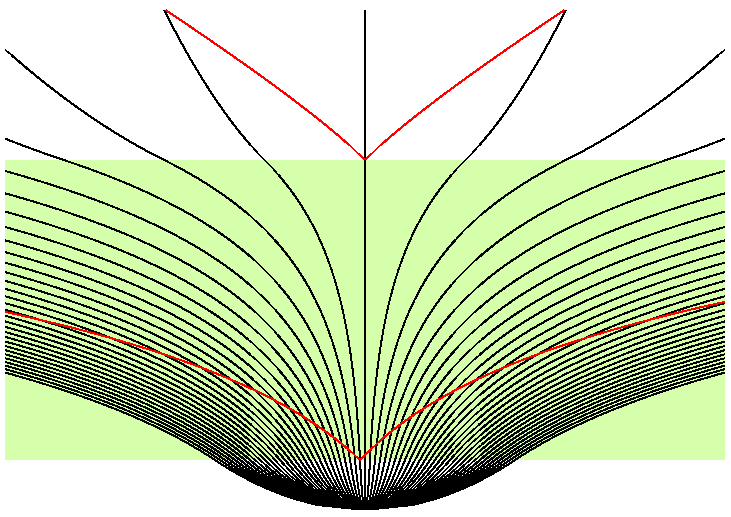
This space-time diagram shows the inflationary epoch tinted green,
and the future lightcones of two events in red. The early event
has a future lightcone that covers a huge area, that can easily
encompass all of our horizon. Thus we can explain why the temperature
of the microwave background is so uniform across the sky.
Details: Large-Scale Structure and Anisotropy
Of course the Universe is not really homogeneous, since it contains
dense regions like galaxies and people. These dense regions should
affect the temperature of the microwave background.
Sachs and Wolfe (1967, ApJ, 147, 73) derived the effect of the
gravitational potential perturbations on the CMB. The
gravitational potential,
phi = -GM/r, will be negative in dense lumps, and positive in
less dense regions. Photons lose energy when they climb out of
the gravitational potential wells of the lumps:
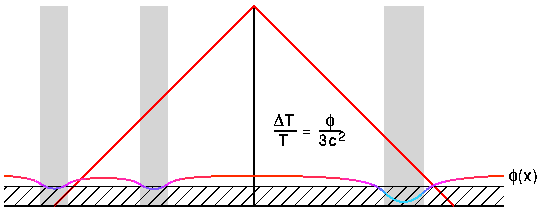
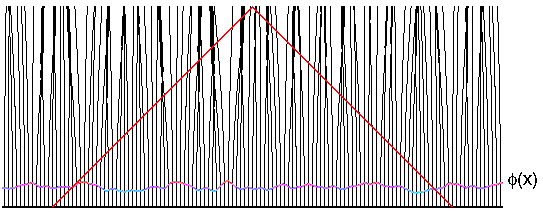
This conformal space-time diagram above shows lumps as gray vertical
bars, the epoch before recombination as the hatched region, and
the gravitational potential as the color-coded curve phi(x). Where
our past lightcone intersects the surface of recombination, we see
a temperature perturbed by dT/T = phi/(3*c2).
Sachs and Wolfe predicted temperature fluctuations dT/T as large
as 1 percent, but we know now that the Universe is far more
homogeneous than Sachs and Wolfe thought. So observers worked
for years to get enough sensitivity to see the temperature
differences around the sky. The first anisotropy to be detected was the
dipole anisotropy by Conklin in 1969:

The map above is from
COBE
and is much better than Conklin's 2 standard deviation detection.
The red part of the sky is hotter by (v/c)*To, while the blue
part of the sky is colder by (v/c)*To,
where the inferred velocity is
v = 370 km/sec. This is how we measure the velocity of the Solar System
relative to the observable Universe.
It was another 23 years before the anisotropy predicted by Sachs and Wolfe
was detected by Smoot \etal in 1992. The amplitude was 1 part in
100,000 instead of 1 part in 100:
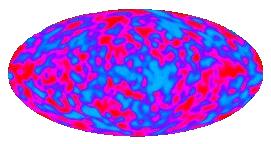
The map above shows cosmic anisotropy (and detector noise) after
the dipole pattern and the radiation from the Milky Way have been
subtracted out.
The anisotropy in this map has an RMS value of 30 microK, and if it is
converted into a gravitational potential using Sachs and Wolfe's result
and that potential is then expressed as a height assuming a constant
acceleration of gravity equal to the gravity on the Earth, we get a
height of twice the distance from the Earth to the Sun. The "mountains
and valleys" of the Universe are really quite large.
Inflation predicts a certain statistical pattern in the anisotropy.
The quantum fluctuations normally effect very small regions of space,
but the huge exponential expansion during the inflationary epoch
makes these tiny regions observable.

The space-time diagram on the left above shows the future lightcones
of quantum fluctuation events. The top of this diagram is really a
volume which intersects our past lightcone making the sky. The
future lightcones of events become circles on the sky. Events
early in the inflationary epoch make large circles on the sky, as
shown in the bottom map on the right. Later events make smaller circles
as shown in the middle map, but there are more of them so the sky coverage
is the same as before. Even later events make many small circles which
again give the same sky coverage as seen on the top map.
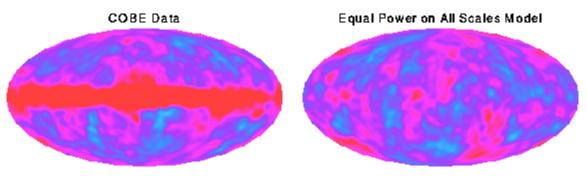
The pattern formed by adding
all of the effects from events of all ages is known as
"equal power on all scales", and it agrees with the COBE data.
Having found that the observed pattern of anisotropy is consistent
with inflation, we can also ask whether the amplitude implies
gravitational forces large enough to produce the observed clustering
of galaxies.
The conformal space-time diagram above shows the phi(x) at recombination
determined by COBE's dT data, and the worldlines of galaxies which are
perturbed by the gravitational forces produced by the gradient of the
potential. Matter flows "downhill" away from peaks of the potential
(red spots on the COBE map), producing voids in the current distribution
of galaxies, while valleys in the potential (blue spots) are where the
clusters
of galaxies form.
COBE
was not able to see spots as small as clusters or even superclusters
of galaxies, but if we use "equal power on all scales" to extrapolate
the COBE data to smaller scales, we find that the gravitational forces
are large enough to produce the observed clustering, but only if these
forces are not opposed by other forces. If the all the matter
in the Universe is made out of the ordinary chemical elements, then
there was a very effective opposing force before recombination,
because the free electrons which are now bound into atoms were very
effective at scattering the photons of the cosmic background.
We can therefore conclude that most of the matter in the Universe
is
"dark matter" that does not emit, absorb or scatter light.
This strange conclusion will be greatly strengthened by temperature
anisotropy data at smaller angular scales which will be
provided by the
Microwave Anisotropy Probe (MAP)
in the year 2000.
Ned Wright's home page
FAQ |
Tutorial :
Part 1 |
Part 2 |
Part 3 |
Part 4 |
Age |
Distances |
Bibliography |
Relativity
© 1996-1998 Edward
L. Wright. Last modified 7-Dec-1998









