Recently two different groups have measured the apparent brightness of supernovae with redshifts near z = 1. Based on this data the old idea of a cosmological constant is making a comeback.
Einstein's original cosmological model was a static, homogeneous model with spherical geometry. The gravitational effect of matter caused an acceleration in this model which Einstein did not want, since at the time the Universe was not known to be expanding. Thus Einstein introduced a cosmological constant into his equations for General Relativity. This term acts to counteract the gravitational pull of matter, and so it has been described as an anti-gravity effect.
Why does the cosmological constant behave this way?
This term acts like a vacuum energy density, an idea which has become quite fashionable in high energy particle physics models since a vacuum energy density of a specific kind is used in the Higgs mechanism for spontaneous symmetry breaking. Indeed, the inflationary scenario for the first picosecond after the Big Bang proposes that a fairly large vacuum energy density existed during the inflationary epoch. The vacuum energy density must be associated with a negative pressure because:
But in General Relativity, pressure has weight, which means that the gravitational acceleration at the edge of a uniform density sphere is not given by
g = GM/R2 = (4*pi/3)*G*rho*Rbut is rather given by
g = (4*pi/3)*G*(rho+3P/c2)*RNow Einstein wanted a static model, which means that g = 0, but he also wanted to have some matter, so rho > 0, and thus he needed P < 0. In fact, by setting
rho(vacuum) = 0.5*rho(matter)he had a total density of 1.5*rho(matter) and a total pressure of -0.5*rho(matter)*c2 since the pressure from ordinary matter is essentially zero (compared to rho*c2). Thus rho+3P/c2 = 0 and the gravitational acceleration was zero,
g = (4*pi/3)*G*(rho(matter)-2*rho(vacuum))*R = 0allowing a static Universe.
However, there is a basic flaw in this Einstein static model: it is unstable - like a pencil balanced on its point. For imagine that the Universe grew slightly: say by 1 part per million in size. Then the vacuum energy density stays the same, but the matter energy density goes down by 3 parts per million. This gives a net negative gravitational acceleration, which makes the Universe grow even more! If instead the Universe shrank slightly, one gets a net positive gravitational acceleration, which makes it shrink more! Any small deviation gets magnified, and the model is fundamentally flawed.
In addition to this flaw of instability, the static model's premise of a static Universe was shown by Hubble to be incorrect. This led Einstein to refer to the cosmological constant as his greatest blunder, and to drop it from his equations. But it still exists as a possibility -- a coefficient that should be determined from observations or fundamental theory.
The equations of quantum field theory describing interacting particles and anti-particles of mass M are very hard to solve exactly. With a large amount of mathematical work it is possible to prove that the ground state of this system has an energy that is less than infinity. But there is no obvious reason why the energy of this ground state should be zero. One expects roughly one particle in every volume equal to the Compton wavelength of the particle cubed, which gives a vacuum density of
rho(vacuum) = M4c3/h3 = 1013 [M/proton mass]4 gm/ccFor the highest reasonable elementary particle mass, the Planck mass of 20 micrograms, this density is more than 1091 gm/cc. So there must be a suppression mechanism at work now that reduces the vacuum energy density by at least 120 orders of magnitude.
We don't know what this mechanism is, but it seems reasonable that suppression by 122 orders of magnitude, which would make the effect of the vacuum energy density on the Universe negligible, is just as probable as suppression by 120 orders of magnitude. And 124, 126, 128 etc. orders of magnitude should all be just as probable as well, and all give a negligible effect on the Universe. On the other hand suppressions by 118, 116, 114, etc. orders of magnitude are ruled out by the data. Unless there is data to rule out suppression factors of 122, 124, etc. orders of magnitude then the most probable value of the vacuum energy density is zero.
If the supernova data and the CMB data are correct, then the vacuum density is about 75% of the total density now. But at redshift z=2, which occurred 11 Gyr ago for this model if Ho = 65, the vacuum energy density was only 10% of the total density. And 11 Gyr in the future the vacuum density will be 96% of the total density. Why are we alive coincidentally at the time when the vacuum density is in the middle of its fairly rapid transition from a negligible fraction to the dominant fraction of the total density? If, on the other hand, the vacuum energy density is zero, then it is always 0% of the total density and the current epoch is not special.
During the inflationary epoch, the vacuum energy density was large: around 1071 gm/cc. So in the inflationary scenario the vacuum energy density was once large, and then was suppressed by a large factor. So non-zero vacuum energy densities are certainly possible.
One way to look for a vacuum energy density is to study the orbits of particles moving in the gravitational field of known masses. Since we are looking for a constant density, its effect will be greater in a large volume system. The Solar System is the largest system where we really know what the masses are, and we can check for the presence of a vacuum energy density by a careful test of Kepler's Third Law: that the period squared is proportional to the distance from the Sun cubed. The centripetal acceleration of a particle moving around a circle of radius R with period P is
a = R*(2*pi/P)2which has to be equal to the gravitational acceleration worked out above:
a = R*(2*pi/P)2 = g = GM(Sun)/R2 - (8*pi/3)*G*rho(vacuum))*RIf rho(vacuum) = 0 then we get
(4*pi2/GM)*R3 = P2which is Kepler's Third Law. But if the vacuum density is not zero, then one gets a fractional change in period of
dP/P = (4*pi/3)*R3*rho(vacuum)/M(sun) = rho(vacuum)/rho(bar)where the average density inside radius R is rho(bar) = M/((4*pi/3)*R3). This can only be checked for planets where we have an independent measurement of the distance from the Sun. The Voyager spacecraft allowed very precise distances to Uranus and Neptune to be determined, and Anderson et al. (1995, ApJ, 448, 885) found that dP/P = (1+/-1) parts per million at Neptune's distance from the Sun. This gives us a Solar System limit of
rho(vacuum) = (5+/-5)*10-18 < 2*10-17 gm/cc
The cosmological constant will also cause a precession of the perihelion of a planet. Cardona and Tejeiro (1998, ApJ, 493, 52) claimed that this effect could set limits on the vacuum density only ten or so times higher than the critical density, but their calculation appears to be off by a factor of 3 trillion. The correct advance of the perihelion is 3*rho(vacuum)/rho(bar) cycles per orbit. Because the ranging data to the Viking landers on Mars is so precise, a very good limit on the vacuum density is obtained:
rho(vacuum) < 2*10-19 gm/cc
In larger systems we cannot make part per million verifications of the standard model. In the case of the Sun's orbit around the Milky Way, we only say that the vacuum energy density is less than half of the average matter density in a sphere centered at the Galactic Center that extends out to the Sun's distance from the center. If the vacuum energy density were more than this, there would be no centripetal acceleration of the Sun toward the Galactic Center. But we compute the average matter density assuming that the vacuum energy density is zero, so to be conservative I will drop the "half" and just say
rho(vacuum) < (3/(4*pi*G))(v/R)2 = 3*10-24 gm/ccfor a circular velocity v = 220 km/sec and a distance R = 8.5 kpc.
The best limit on the vacuum energy density comes from the largest possible system: the Universe as a whole. The vacuum energy density leads to an accelerating expansion of the Universe. If the vacuum energy density is greater than the critical density, then the Universe will not have gone through a very hot dense phase when the scale factor was zero (the Big Bang). We know the Universe went through a hot dense phase because of the light element abundances and the properties of the cosmic microwave background. These require that the Universe was at least a billion times smaller in the past than it is now, and this limits the vacuum energy density to
rho(vacuum) < rho(critical) = 8*10-30 gm/ccThe recent supernova results suggest that the vacuum energy density is close to this limit: rho(vacuum) = 0.75*rho(critical) = 6*10-30 gm/cc. The ratio of rho(vacuum) to rho(critical) is called lambda. This expresses the vacuum energy density on the same scale used by the density parameter Omega. Thus the supernova data suggest that lambda = 0.75. If we use OmegaM to denote the ratio of ordinary matter density to critical density, then the Universe is open if OmegaM + lambda is less than one, closed if it is greater than one, and flat if it is exactly one. If lambda is greater than zero, then the Universe will expand forever unless the matter density OmegaM is much larger than current observations suggest. For lambda greater than zero, even a closed Universe can expand forever.

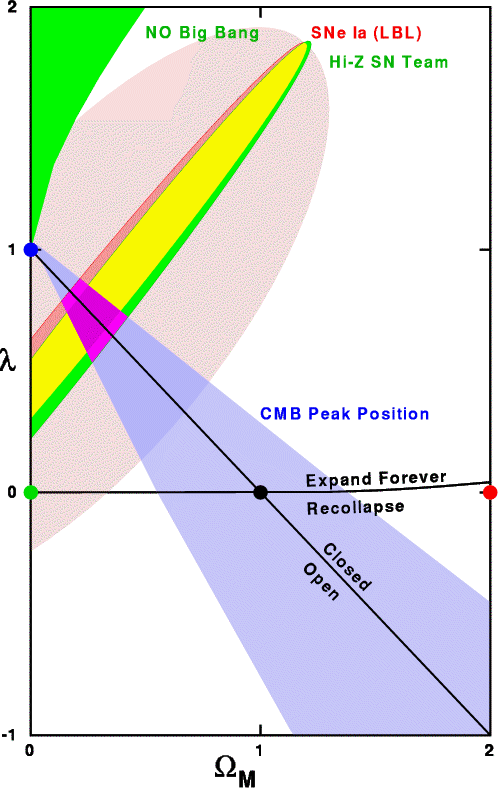
The figure above shows the regions in the (OmegaM, lambda) plane that are suggested by the current data. The green region in the upper left is ruled out because there would not be a Big Bang in this region leaving the CMB spectrum unexplained. The red and green ellipses with yellow overlap region show the LBL team's allowed parameters (red) and the Hi-Z SN Team's allowed parameters (green). The blue wedge shows the parameter space region that gives the observed Doppler peak position in the angular power spectrum of the CMB. The purple region is consistent with the CMB Doppler peak position and the supernova data. The big pink ellipse shows the possible systematic errors in the supernova data.
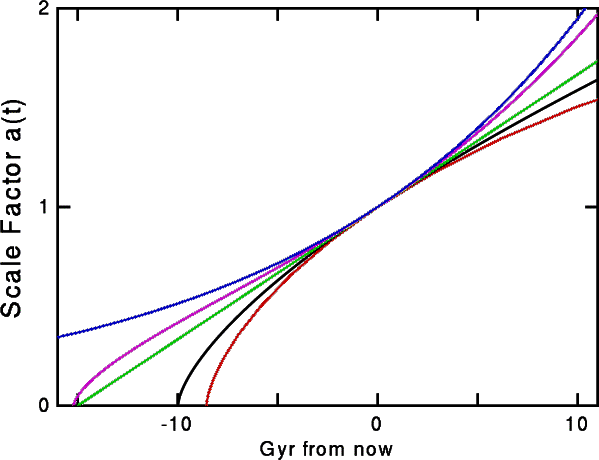
The figure above shows the scale factor as a function of time for several different models. The colors of the curves are keyed to the colors of the circular dots in the (OmegaM, lambda) plane Figure. The purple curve is for the favored OmegaM = 0.25, lambda = 0.75 model. The blue curve is the Steady State model, which has lambda = 1 but no Big Bang.
Because the time to reach a given redshift is larger in the OmegaM = 0.25, lambda = 0.75 model than in the OmegaM = 1 model, the angular size distance and luminosity distance are larger in the lambda model, as shown in the space-time diagram below:
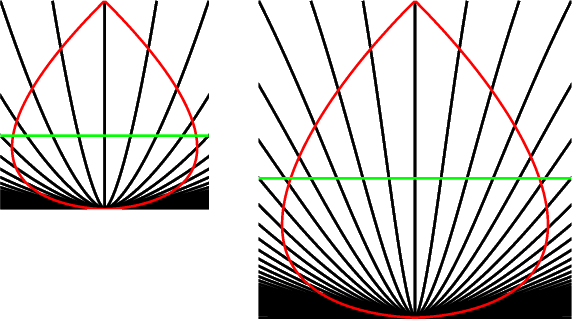
The OmegaM = 1 model is on the left, the OmegaM = 0.25, lambda = 0.75 model is on the right. The green line across each space-time diagram shows the time when the redshift was z = 1, which corresponds to approximately to the most distant of the supernovae observed to date. Using a ruler you can see that the angular size distance to z = 1 is 1.36 times larger in the right hand diagram, which makes the observed supernovae 1.84 times fainter (0.66 magnitudes fainter).
In the past, we have had only upper limits on the vacuum density and philosophical arguments based on the Dicke coincidence problem and Bayesian statistics that suggested that the most likely value of the vacuum density was zero. Now we have the supernova data that suggests that the vacuum energy density is greater than zero. This result is very important if true. We need to confirm it using other techniques, such as the MAP satellite which will observe the anisotropy of the cosmic microwave background with angular resolution and sensitivity that are sufficient to measure the vacuum energy density.
FAQ | Tutorial : Part 1 | Part 2 | Part 3 | Part 4 | Age | Distances | Bibliography | Relativity
© 1998 Edward L. Wright. Last modified 8-Apr-1998