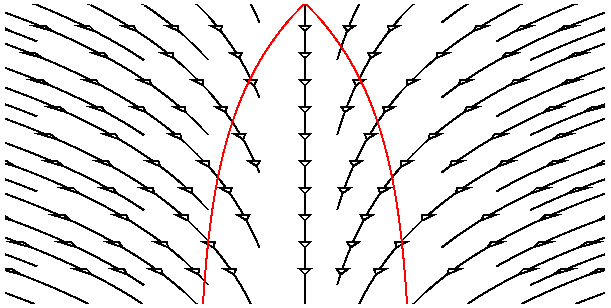
The Steady State model of the Universe was proposed in 1948 by Bondi and Gold and by Hoyle. Bondi and Gold adopted the "Perfect Cosmological Principle", and added the assumption that the Universe was the same at all times to homogeneity (the same in all places) and isotropy (the same in all directions). At the time the Steady State model was proposed, the Big Bang model was in trouble because the value of the Hubble constant was clearly bigger than the inverse of the age of the Universe. [Sound familiar?] If the Universe is the same at all times, the value of the Hubble constant must really be constant, so v = dD/dt = HD has an exponential solution and the scale factor varies like
a(t) = exp(H(to-t))Furthermore, since the radius of curvature of the Universe can not change, but must expand, the radius has to be infinite. Thus the Steady State model has flat spatial sections like the critical density Big Bang model. Since the expansion of the Universe spreads the existing matter over a larger and larger volume, but the density stays constant, the Steady State model requires continuous creation of matter. The average age of matter in the Steady State model is <t> = 1/(3*Ho) but some galaxies are much older than the average, so the age of the globular clusters can be accomodated if the Milky Way is older than the average. The space-time diagram below shows the Steady State model:

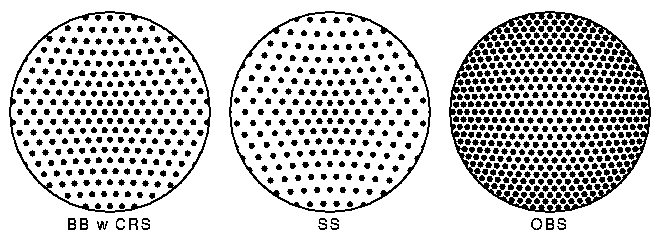
The Steady State model makes some definite predictions. The first
one to be tested involved the number of faint radio sources.
In the 1950's astronomers found that radio sources were typically
much more distant than typical optical galaxies, so modifications
to the usual source count law due to cosmology were expected. For
the standard Big Bang model the counts were expected to fall below
the usual "8 times more sources for 4 times fainter limit" law by
an amount given approximately by 1/(1+z)4
where z is the redshift of the sources.
This law assumes that radio sources are conserved, so a given section
of the Universe has the same number of radio sources at all times.
Because the volume of the section was smaller by a factor of (1+z)3
at early times, the actual density of radio sources was higher by
a factor of (1+z)3. The density was constant in the Steady State
model, of course, so the count correction factor would be given
by 1/(1+z)7. The diagram below shows what was expected and
actually seen:
 The discovery of the cosmic background blackbody radiation came later,
and completed the death of the Steady State. The Universe now
is not producing a blackbody since it is not isothermal and it is transparent
instead of opaque. In the Steady State the Universe was always the same so
it never produced a blackbody. Hence the existence of a blackbody
background ruled out the Steady State.
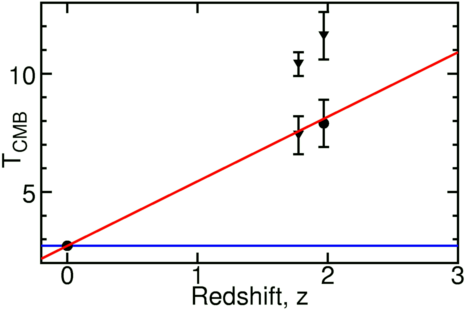
In addition, the temperature of the cosmic background can be measured in some
very distant clouds that produce absorption lines in the spectra of
quasars. The neutral carbon atoms in these clouds are excited to an
excitation temperature that can be measured using line ratios.
These excitation temperatures are upper limits to the CMB temperature
and are shown as triangular data points at right.
In some clouds corrections for other sources of excitation can be made,
giving a direct measure of TCMB, shown as a round data point.
This data agrees very well with the evolution expected in the Big Bang
model: TCMB = To(1+z), which is shown as
the red line in the figure.
Even if there were some unknown mechanism for producing a blackbody radiation
field in the Steady State model, its temperature would have to constant
as a function of redshift as shown by the blue
line and these observations reject this model.
The discovery of the cosmic background blackbody radiation came later,
and completed the death of the Steady State. The Universe now
is not producing a blackbody since it is not isothermal and it is transparent
instead of opaque. In the Steady State the Universe was always the same so
it never produced a blackbody. Hence the existence of a blackbody
background ruled out the Steady State.
In addition, the temperature of the cosmic background can be measured in some
very distant clouds that produce absorption lines in the spectra of
quasars. The neutral carbon atoms in these clouds are excited to an
excitation temperature that can be measured using line ratios.
These excitation temperatures are upper limits to the CMB temperature
and are shown as triangular data points at right.
In some clouds corrections for other sources of excitation can be made,
giving a direct measure of TCMB, shown as a round data point.
This data agrees very well with the evolution expected in the Big Bang
model: TCMB = To(1+z), which is shown as
the red line in the figure.
Even if there were some unknown mechanism for producing a blackbody radiation
field in the Steady State model, its temperature would have to constant
as a function of redshift as shown by the blue
line and these observations reject this model.
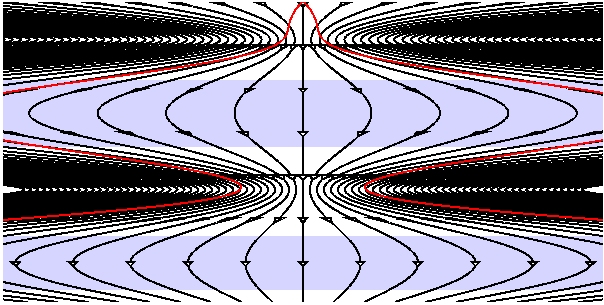
The Quasi-Steady State Cosmology is an attempt by Hoyle, Burbidge
and Narlikar to allow for the evolution of the CMB temperature
and to explain the surplus of faint radio sources in a
Universe that is always the same over the very long term. A
sinusoidal pulsation is superimposed over the exponential growth
of the scale factor a(t), giving the space-time diagram below.
Tutorial:
Part 1 |
Part 2 |
Part 3 |
Part 4
FAQ |
Age |
Distances |
Bibliography |
Relativity
© 1997-2000 Edward L. Wright. Last modified 2 Mar 2000